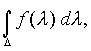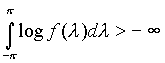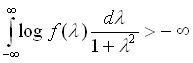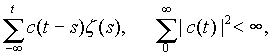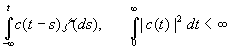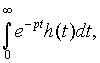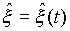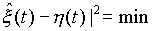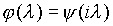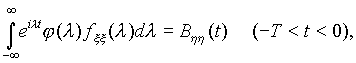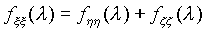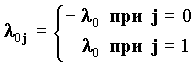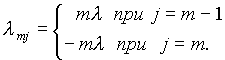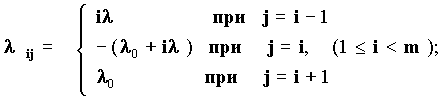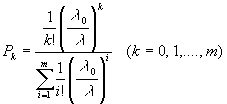|
|
|||||
|
10.20 Справочные данные по математике
Семенов Ю.А. (ГНЦ ИТЭФ) |
|||||
Приводимые в данном разделе определения вляются "шпаргалкой" на случай, когда вы знаете предмет, но что-то забыли. Для первичного изучения математических основ рекомендую обратиться к серьезным монографиям и учебникам. Условная вероятность .В теории вероятностей характеристикой связи событий А и B служит условная вероятность P(А|B) события А при условии B, определяемая как P(А|B) =
Если событие B ведет к обязательному осуществлению А:
b
Если имеется полная система несовместимых событий B =B1, B2,. т.е. такая система непересекающихся событий, одно из которых обязательно осуществляется, то вероятность события A (P(A)) выражается через условные вероятности P(A|B) следующим образом:
Множества .
Множество
- это совокупность некоторых элементов. Если элемент х входит в множество А, это записывается как x О A. Соотношения A1 Н A2 или A2
К A1 означает, что A1 содержится во множестве A2 (каждый элемент х множества A1 входит в множество A2;
A1 является подмножеством A2).
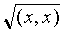 .
.Счетно-гильбертово пространство Х называется ядерным , если для любого р найдется такое q и такой ядерный оператор А в гильбертовом пространстве Х со скалярным произведением (х1,x2)=(х1,х2)q, что (х1,x2)p=(Ax1,x2)q. Действительное число M является
верхней границей
или
нижней границей
множества Sy
действительных чисел y, если для всех y
О Sy
соответственно y ё M или yЁ M. Множество действительных или комплексных чисел
ограничено
(имеет абсолютную границу), если верхнюю границу имеет множество абсолютных величин этих чисел; в противном случае множество не ограничено. Каждое непустое
множество Sy
действительных чисел y, имеющее верхнюю границу, имеет
точную верхнюю границу
(наименьшую верхнюю границу) sup y, а каждое непустое множество действительных чисел y, имеющее нижнюю границу, имеет
точную нижнюю
границу
(наибольшую нижнюю границу) inf y. Если множество Sy
конечно, то его точная верхняя граница sup y необходимо равна наибольшему значению (максимуму) max y, фактически принимаемому числом y в Sy
, а точная нижняя граница inf y равна минимуму min y.
Компакт.
Система множеств G называется
центрированной
, если пересечение конечного числа любых множеств из G не пусто. Замкнутое множество A Н X называется
компактом
, если всякая центрированная система G его замкнутых подмножеств F имеет непустое пересечение: Гауссовы случайные процессы . Действительная случайная величина x называется гауссовой, если ее характеристическая функция j =j (u) имеет вид
Марковские случайные процессы . Случайный процесс x =x(t) на множестве T действительной прямой в фазовом пространстве ( E,B ) называется марковским, если условные вероятности P(A| U (-╔,s) событий AО U (t,╔ ) относительно s-алгебры U (-╔,s) таковы, что при s ёt с вероятностью 1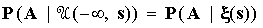 , ,здесь U (u,v) означает s-алгебру порождаемую всевозможными событиями вида { x(t) О B}, t О[u,v]З T, BО B . Если параметр t интерпретировать как время, то описанное марковское свойство случайного процесса x =x (t) состоит в том, что поведение процесса после момента t при фиксированном состоянии x= x (t) не зависит от поведения процесса до момента t. Для любых событий А О U (-╔,t1) и A2 О U (t1, ╔) и при любом t О T t1 ёtё t2 с вероятностью 1 P(A1A2|x (t)) = P(A1|x (t)) P(A2|x(t)). Цепи Маркова . Пусть x (t) - состояние системы в момент времени t, и пусть соблюдается следующая закономерность: если в данный момент времени s система находится в фазовом состоянии i, то в последующий момент времени t система будет находиться в состоянии j с некоторой вероятностью pij(s,t) независимо от поведения системы до указанного момента s. Описывающий поведение системы процесс x (t) называется цепью Маркова. Вероятности pij(s,t) = p{x (t)=j|x (s)=i} (i,j = 1, 2, .) называются переходными вероятностями марковской цепи x (t).Марковская цепь x (t) называется однородной , если переходные вероятности pij(s,t) зависят лишь от разности t-s: pij(s,t) = pij(s-t) (i,j=1,2,.) Финальные вероятности . Пусть состояния однородной марковской цепи x (t) образует один замкнутый положительный непериодический класс. Тогда для любого состояния j существует предел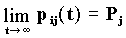 (j=1, 2,.), один и тот же при всех исходных состояниях i=1,2,.. Предельные значения P1, P2,. представляют собой распределение вероятностей: pj есть финальная вероятность находиться в состоянии j; при этом
(j=1, 2,.), один и тот же при всех исходных состояниях i=1,2,.. Предельные значения P1, P2,. представляют собой распределение вероятностей: pj есть финальная вероятность находиться в состоянии j; при этом Pj= 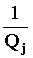 (j=1,2,...),
(j=1,2,...),где Qj - среднее время возвращения в состояние j в дискретные моменты t = 0, 1, 2, . . Коэффициент эргодичности . Пусть x =x (t) - случайный марковский процесс в фазовом пространстве (E, B ) с переходной функцией P(s,x,t,B). С вероятностью 1 имеет место равенство
b
(s,t) =
Величина k(s,t) = 1 -
называется коэффициентом эргодичности марковского процесса x =x (t). Переходная функция. Функция P(s,x,t,B) переменных s, tО T, s ё t и xО E, bО b называется переходной функцией марковского случайного процесса x =x (t) на множестве T в фазовом пространстве (E, B ), если эта функция при фиксированных s, tО T и xО E представляет собой распределение вероятностей на s -алгебре b и при фиксированных s, tО T и BО b является измеримой функцией от x О E.Стационарные случайные процессы . Стационарный действительный или комплексный случайный процесс x =x (t), рассматриваемый как функция параметра t со значениями в гильбертовом пространстве L2(W) всех действительных или комплексных случайных величин h =h (w), M|h |2<╔ (со скалярным произведением(h 1, h 2)= M h 1 h 2), может быть представлен в виде
Белый шум. Простейшим по структуре стационарным процессом с дискретным временем является процесс z =z (t) с некоррелированными значениями:Mz(t)=0, M|z(t)|2=1, В случае непрерывного времени t аналогом такого процесса является так называемый "белый шум" - обобщенный стационарный процесс z = б u, z с вида
Mz (D )=0, M|z (D )|2 =t-s при D =(s,t), Mz (D 1) z (D 2)=0 для любых непересекающихся D 1 и D 2. Стационарный процесс x=
x(t), Mx(t)=0, называется линейно-регулярным, если
Стационарный процесс x =x(t) линейно-регулярен тогда и только тогда, когда он получается некоторым физически осуществимым линейным преобразованием из процесса z = z(t) с некоррелированными значениями - в случае дискретного t:
x(t) =
и из процесса z =б u, z с "белого шума" - в случае непрерывного t:
x(t) =
Регулярность . Реальные стационарные процессы часто возникают в результате некоторого случайного стационарного возмущения Z = z (t) типа "белого шума". Процесс z = z(t) подвергается некоторому линейному преобразованию и превращается в стационарный процесс x =x(t). Спектральная плотность f= f(l) такого процесса в диапазоне -p ё l ё p для целочисленного времени и -╔ <l <╔ для непрерывного времени t не может обращаться тождественно в нуль ни на каком интервале: в противном случае стационарный процесс x (t) будет сингулярным, что означает возможность его восстановления лишь на полуоси -╔ ,t0. Процессы, спектр которых практически сосредоточен в полосе частот -W< l <W, не обладают свойствами сингулярных процессов. С энергетической точки зрения эти процессы имеют ограниченный спектр. Составляющие их гармонические колебания вида Ф(dl )eilt с частотами вне интервала (-W,W) имеют весьма малые энергии, но они существенно влияют на линейный прогноз значений x (t+t) на основе x (s) на временной полуоси sёt. Линейные устройства, используемые при решении конкретных задач, должны иметь вполне определенную постоянную времени T (определяет длительность переходных процессов). Это означает, что весовая функция h=h(t) рассматриваемого линейного устройства, связанная с соответствующей передаточной функцией Y =Y(p) равенством Линейное устройство, отвечающее поставленным требованиям, должно иметь такую передаточную функцию Y=Y(p), чтобы соответствующая спектральная характеристика Где Закон больших чисел . Пусть x 1,., x n - независимые случайные величины, имеющие одно и то же распределение вероятностей, в частности одни и те же математические ожидания a = M x k и дисперсииs 2=Dx k, k=1,.,n. Каковы бы ни были e >0 и d >0, при достаточно большом n арифметическое среднее 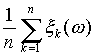 (таким образом
(таким образом
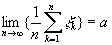 )
) с вероятностью, не меньшей 1-d, будет отличаться от математического ожидания a лишь не более чем на 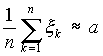
Распределение Эрланга Рассмотрим систему, которая способна обслуживать m запросов одновременно. Предположим, что имеется m линий и очередной запрос поступает на одну из них, если хотя бы одна из них свободна. В противном случае поступивший запрос будет отвергнут. Поток запросов считается пуассоновским с параметром l 0 , а время обслуживания запроса (в каждом из каналов) распределено по показательному закону с параметром l , причем запросы обслуживаются независимо друг от друга. Рассмотрим состояния E0, E1,.,Em, где Ek означает, что занято k линий. В частности E0 означает, что система свободна, а Em - система полностью занята. Переход из одного состояния в другое представляет собой марковский процесс, для которого плотности перехода можно описать как:
При t ╝ ╔ переходные вероятности pij(t) экспоненциально стремятся к своим окончательным значениям Pj, j=0,.,m. Окончательные вероятности Pj могут быть найдены из системы: -l 0P0+lP1=0 l 0Pk-1 - (l 0+kl)Pk + (k+1)lPk+1 =0 (1ё k<m) l 0pm-1+ml Pm=0 решение которой имеет вид:
Эти выражения для вероятностей называются формулами (распределением) Эрланга. |
|||||
|
Previous:
10.19 Символьный набор HTML
UP:
10.11 Адреса серверов ведущих фирм, работающих в сфере телекоммуникаций
|
|||||

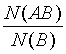 ,
,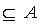 , то P(A|B)=1, если же
наступление B исключает возможность события А:
A*B=0, то P(A|B)=0. Если событие А представляет собой объединение непересекающихся событий A1, A2,.: A =
, то P(A|B)=1, если же
наступление B исключает возможность события А:
A*B=0, то P(A|B)=0. Если событие А представляет собой объединение непересекающихся событий A1, A2,.: A =
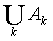 ,
то P(A|B) =
,
то P(A|B) =
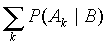 .
.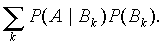
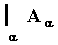 произвольного числа множеств Аa состоит из всех точек х, которые одновременно входят во все множества Аa.
произвольного числа множеств Аa состоит из всех точек х, которые одновременно входят во все множества Аa.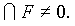 Множество А называется
компактным
в Х,
если его замыкание F=[A] является
компактом
.
Множество А называется
компактным
в Х,
если его замыкание F=[A] является
компактом
.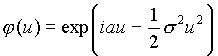 ;
;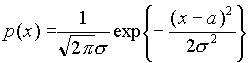
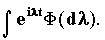
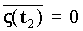 при t1 ≠ t2
при t1 ≠ t2
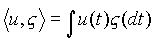
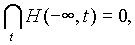 ,
,